一种交互介绍--傅里叶变化

傅里叶变换是一个有趣的工具。这篇文章主要内容是：

解释傅里叶变换的作用
它的变形使用
你如何使用它来做些漂亮的东西

文章之后你会对以下问题有个了解：

什么是傅里叶变换
傅里叶变换的一些实用场景
傅里叶变换的一些毫无意义但是又很cool的用法

我们现在需要先把数学和方程搁置一边，虽然其中蕴含着十分有趣的数学，但是我们最好先从它的实际意义，以及为什么你会使用它开始。

它是啥

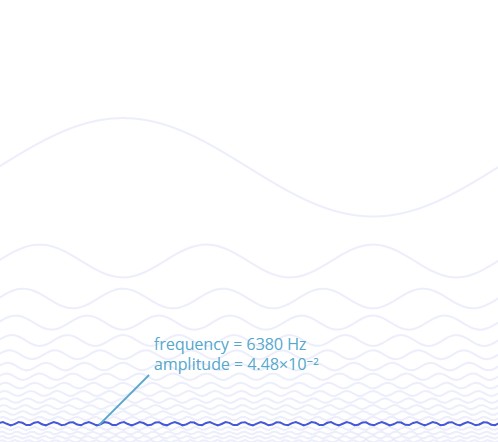
简言之，傅里叶变换是一种将东西分解成正弦波的方式，像往常一样，这个名字的由来是因为很久以前的一个叫傅里叶的人。

让我由一些简单的例子开始，首先，我们看一下波的模式，其随着时间的推移变换。

这里有个例子：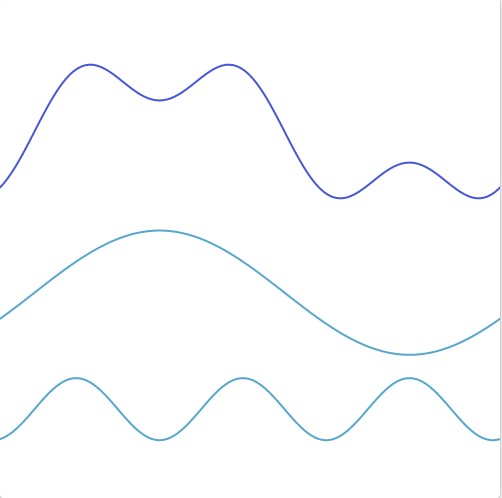

这里的波形图可以分解为正弦波，也就是说，当我们叠加两个正弦图时，我们能得到原始波形图。

傅里叶变换是一种我们用来合成波，或者得到原波形图的正弦波的一种方式，在这个例子中，你几乎可以在脑海中完成这一过程，当你看到原波形图的时候。

为什么呢？我们现实中有许多事物实际上是基于正弦波的。我们通常称它为波的频率。

在这众多的现象中，我们拿声音来举例，当我们听到声音时，我们没有听到波浪线，我们实际上听到的是不同的正弦波频率组成的声响。

我们通过用电脑来分离这些波使我们来了解人们实际听到的是什么。我们可以明白什么是高音，什么是低音，声音的内容又是什么。

我们也可以在看起来不那么像正弦波的波使用这一过程。来看这个方波：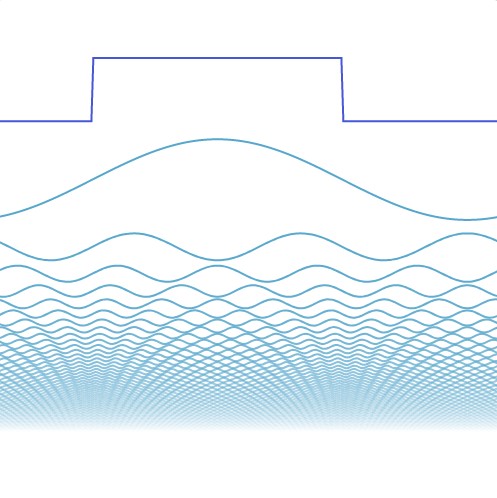

他依然可以被正弦波分解，虽然他看起来和正弦波区别这么大。让我们用技术手段更多的呈现这一过程，当我们加入更多的正弦波的时候，这个波形越来越接近我们开始的方波。视觉上，你会注意到，其实一开始的几个波产生的影响比较大。当波浪再叠加的时候，会看到波形图开始摇摆，当我们继续进行波形的叠加的时候，摇摆会趋于平坦。

当你在听这个声波的时候，你会听到声音变低，因为我们在移除高频。无论你画出什么样的波形图，都可以用正弦波叠加的方式合成它。

我们当然可以通过这样的方式去得到我们最后想要的结果。我们使用傅里叶变换，我们能得到声音最重要的部分，而且存储最后与声音最为相似的部分。通常在计算机上，我们将波存储为一系列的点。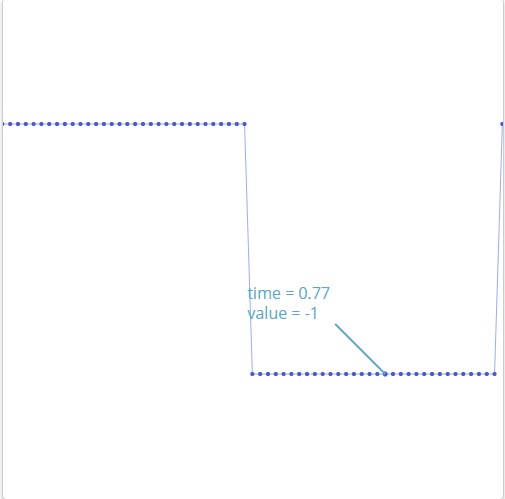

我们能做的是使用一系列的正弦波来表示它，之后我们通过忽略较小的频率来将它压缩，最后得到的结果虽然略有差异，但是他听起来还是极其接近于同一个人的声音。

这就是MP3干的事儿，他知道什么需要存储起来，什么需要抛弃。由此，我们可以使用傅里叶变化去理解波形的基本参数点，然后可以对其进行压缩。现在我们来深入探讨一下傅里叶变换。接下来的模块会十分精彩，但它依旧能使你更深入的认识傅里叶变换。

本轮

现在，我们说把事物分解成正弦波，这里的正弦波不再是一般的正弦波，他们是3D的，你可以称他们为“复杂正弦波”，也可以称他们为“螺旋”。看这边，他们看起来像正弦波，当当我们从正面看时，他们看起来像个圆。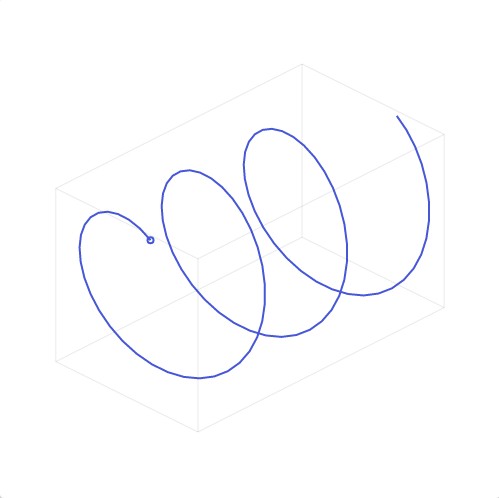

到目前为止，我们所做的一切只需要2D正弦波，当我们对2D波进行傅里叶变换，那些复杂的部分被抛弃，我们最终得到了正弦波。但是我们可以用3D正弦波做出一些有趣的玩意儿。你看：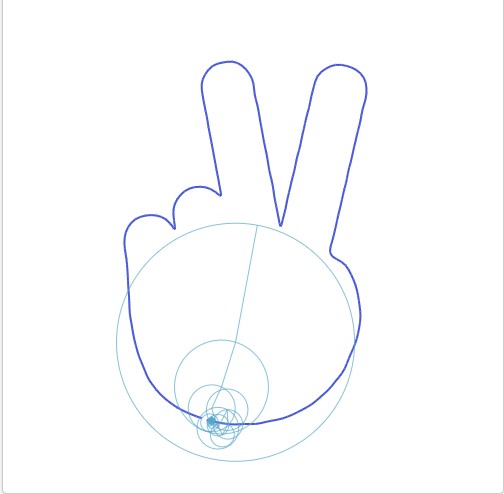

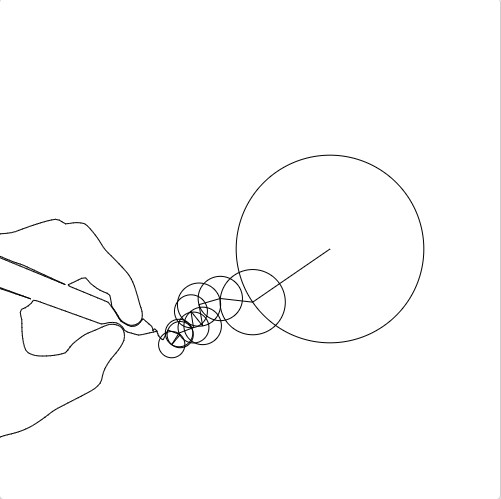
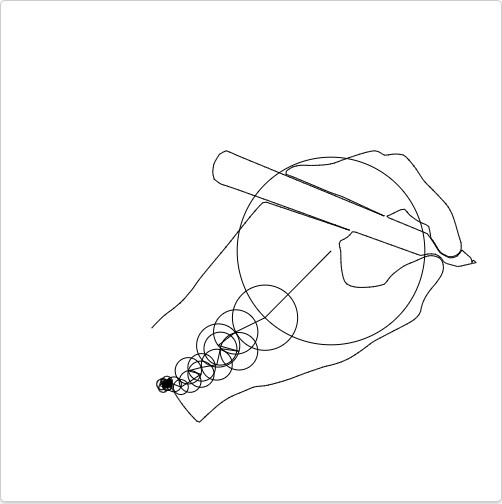
我们可以想象出来这个绘画的3D图，因为他们的移动时随着时间的变化变化的。想象某人画了这个手的图片，其由三个维度的向量代表笔尖此刻的位置。X，Y向量告诉我们位置，时间维度是那个时刻的时间。

现在我们得到了3D模式，我们不能用旧的2D正弦波来表示他，无论用多少2
D正弦波来调试，都永远无法得到3D图形。所以我们需要些别的东西。为何不像之前那样加载一些3D正弦波，当我们加载一定数量的3D正弦波时，我们开始看到像3D模式一样的效果出来。请记得，当我们从正面观看这些波时，他们看上去就是个圆，这种围绕另外一个圆圈旋转的圆圈我们称他们为本轮。

就像之前一样，我们通过一些圆就能很好的还原之前我们设计的图像。因为这是一个简单的图案，所有最后的波形叠加，都是为了使边缘变得平滑，其实所有的图案都可以按照这样的方法进行绘制。

再一次，你所看到的几乎所有图像，都可以用几个圆进行无限的接近它，而不是记录所有的图像点。我们可以使用它作为实际的数据格式。事实上已经存在这样的数据格式了，叫做SVG。

JPEGs

你知道傅里叶变换被用于图像吗？事实上，我们经常使用到他，因为这就是JPEGs工作的方式。我们将其分解成大量的正弦波，然后只储存最重要的那些波形。

我们需要一些不同的正弦波，去使无论我们给出什么样的图像，都能通过添加大量的正弦波把它还原出来。为了做到这一点，我们需要用图像表示成正弦波，我们使用有黑白色彩的图像，我们用每个图片的对比度来表示表示波的大小。我们需要些水平波，一些竖直波。

就他们本身而言是不足以表示成我们想要的图像，所以还需要做一些操作，比如两个图像相乘。8X8的图像，这里有所有我们需要的图像。

当我们调节合适的对比度，之后使他们叠加，我们可以创建任何图像。随着我们添加越来越多的图像，我们最后的结果就越来越接近模型的图像，

图像被分为8X8的块，块与块之间分开，我们使用一组频率来表示像素点的明暗，再用另外两个集合来表示它的颜色，一组是红-绿，一组是黄-蓝。每个块的频率表示了JPEG的质量。