今天我要分享一个想法。这是一个非常简单的想法,它不是那么花哨,当然也不是那么新奇。事实上,我相信很多人早就考虑过这个问题。假设你没有,或者即使你有,我也希望你能花几分钟和我一起享受它。
首先,让我们明确一些信息:每个矩阵对应着一个加权的二分图。
- 图是一个由顶点和边组成的集合。
- 二分是指有两种不同的类型(我将用颜色表示)
- 加权意味着每条边都有一个标记的数字
对于图,一个a 3×2的矩阵 M 中。你会注意到我画了三个绿色的点,每一个表示矩阵 M 对应的每行;还有两个粉色的点,每个点为 M 对应的每列。如果对应的实体在 M 中不为零,我会在绿色和红色的点中间画一条边。

例如,第二个绿色的点和第一个粉色的点之间有一条边,因为 M21 = 4,由此第二行第一列不为零,我将连接这两个点,并对这条边标上数字4。另一方面, M12 = 0 所以它没有边。
请让我更进一步阐明这些设置。
任何矩阵 M 都是由一个 n × m 的数组构成。所以它具备了一些功能,例如:M: X × Y → R :X ={x1,……, xn}为x的集合,定义这是集合 n 的元素。同理集合Y={y1,……, yn}为y的集合,定义这是集合 m 的元素。如果我要描述这个集合 M ,我会向你描述他的每一个 ij 为多少。即,对于每一个 ij 对应的具体数字是多少。所以,这个功能描述了:M: X × Y → R 关联着每一对(xi, yj),得到明确的实数 M(xi, yj)。缩写之后变成: Mij 对应 M (xi, yj)。
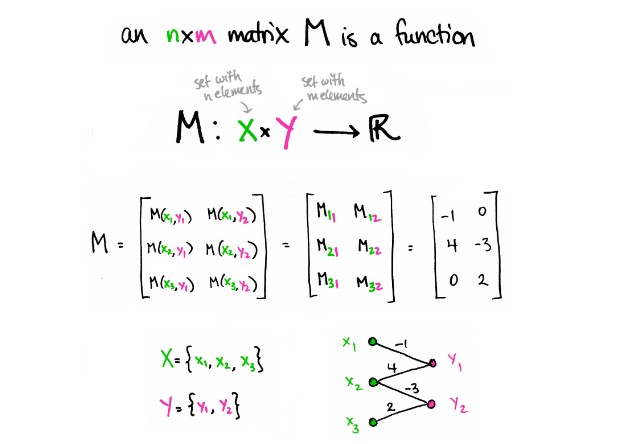
瞧瞧,矩阵是种功能。
将以上条目进行变形, X 的元素作为绿色的点,Y 的元素作为粉色的点。如此,矩阵变形的图,由以下规则进行加权,图的顶点具有两种不同颜色 X, Y,每一条边都连接了xi,yj,之后擦去边上为数字 0 标记的边。
瞧瞧,每个矩阵对应着一个图。
当我们这样可视化矩阵时,会发生美好的事情。例如…
矩阵乘法将会像是漫游图的路径
给出两个矩阵 M: X × Y → R 和 N:Y × Z → R, 我们可以通过把这两个图黏在一起,并沿着路径计算。这里的边连接着 xi 到 zj。计算的时候,数算同一 X 起点到同一 z 点中的路径可能,每个完全的路径进行相乘,并加上不同路径相乘的结果。最后得到新的矩阵,如下图:
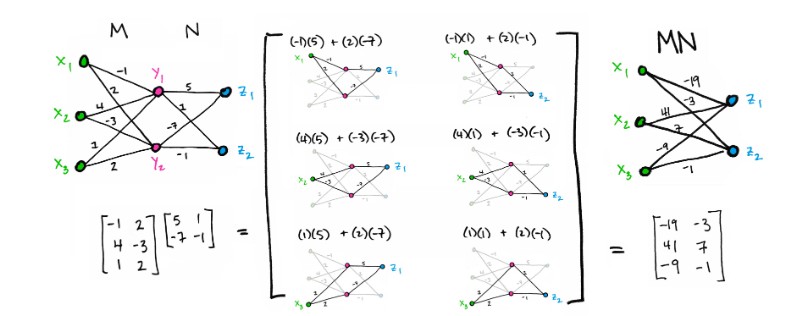
对称矩阵应用于对称图
如果矩阵等于其转置,则矩阵是对称的。你可以在图表中看到这种特性:
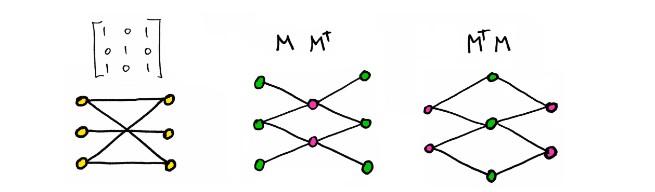
矩阵元素若全为非零,则对应完全二分图
如果矩阵任意元素非零,则意味着对应图中没有缺失的边。
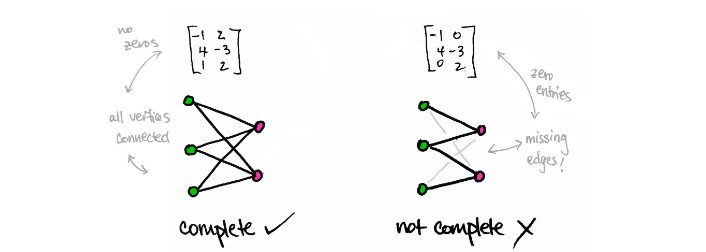
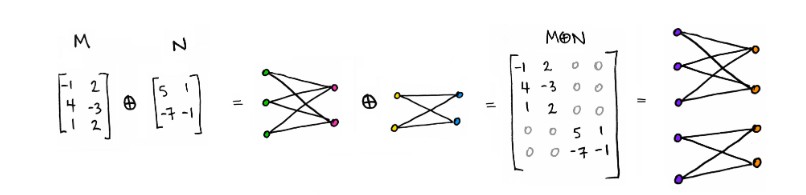
块矩阵对应于断开的图
因为其具有块状的 0 元素块。
概率
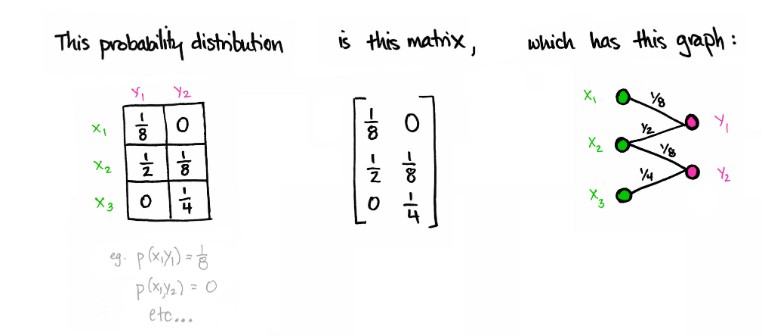
这种概率分布图表使我们能读到一些不错的东西。
联合概率
通过构造,图的边捕获联合概率(xi, yj),就是那连接边上的标签。
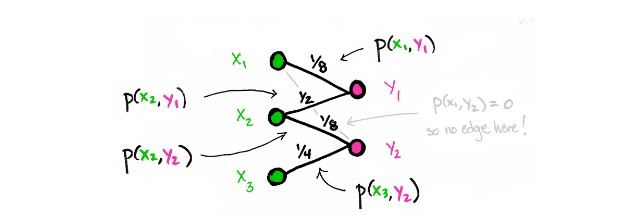
边际概率
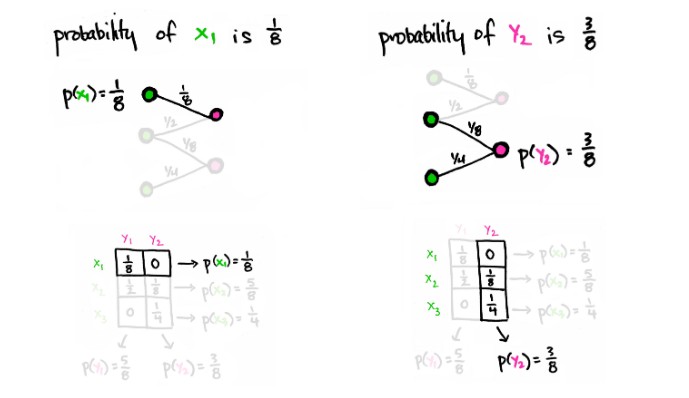
边际概率是通过沿矩阵的行/列求和获得。例如:x1 的概率是 p(x1) = p(x1, y1) + p(x1, y2) = 1/8 + 0 。这是第一行的总和。在图中,xi 的边际概率为,以 xi 为顶点,所有经过的边的总和,yj 的边际概率为,以 yj 为顶点,所有经过该顶点的边的总和。
条件概率
通过将联合概率除以边际概率获得条件概率。

很简单吧? 这里没有任何复杂的东西,但有时候以新的方式看待旧的想法真是太好了!
文章参考

